3. Shallow Neural Networks

3.1 Neural Network Example

浅层神经网络定义一个函数 $y = f[\phi, x]$，其中 $x$ 和 $y$ 分别是多元输入和多元输出，$a(\cdot)$ 表示激活函数（activation function），$\phi$ 表示十个参数的集合：

$$
{ \phi_0, \phi_1, \phi_2, \phi_3, \theta_{10}, \theta_{11}, \theta_{20}, \theta_{21}, \theta_{30}, \theta_{31} }
$$

定义如下函数：

$$
f[x, \phi] = \phi_0 + \phi_1 a[\theta_{10} + \theta_{11}x] + \phi_2 a[\theta_{20} + \theta_{21}x] + \phi_3 a[\theta_{30} + \theta_{31}x]
$$

计算过程分为三步：

1. 计算三个线性函数：
   $$
   \theta_{10} + \theta_{11}x,\quad \theta_{20} + \theta_{21}x,\quad \theta_{30} + \theta_{31}x
   $$

2. 将这三个结果传入激活函数 $a(\cdot)$

3. 将三个激活后的结果与 $\phi_i$ 加权相加得到最终输出

激活函数定义

最常用的激活函数是 ReLU：

$$
a[z] = \text{ReLU}(z) =
\begin{cases}
0, & z < 0 \\
z, & z \ge 0
\end{cases}
$$

3.1.1 Neural Network Intuition

为了让上述函数更加容易理解，我们定义中间变量：

$$
h_1 = a[\theta_{10} + \theta_{11}x] \\
h_2 = a[\theta_{20} + \theta_{21}x] \\
h_3 = a[\theta_{30} + \theta_{31}x]
$$

我们将 $h_1, h_2, h_3$ 称为隐藏单元（hidden units），则最终输出为：

$$
y = \phi_0 + \phi_1 h_1 + \phi_2 h_2 + \phi_3 h_3
$$

函数图像过程：
 

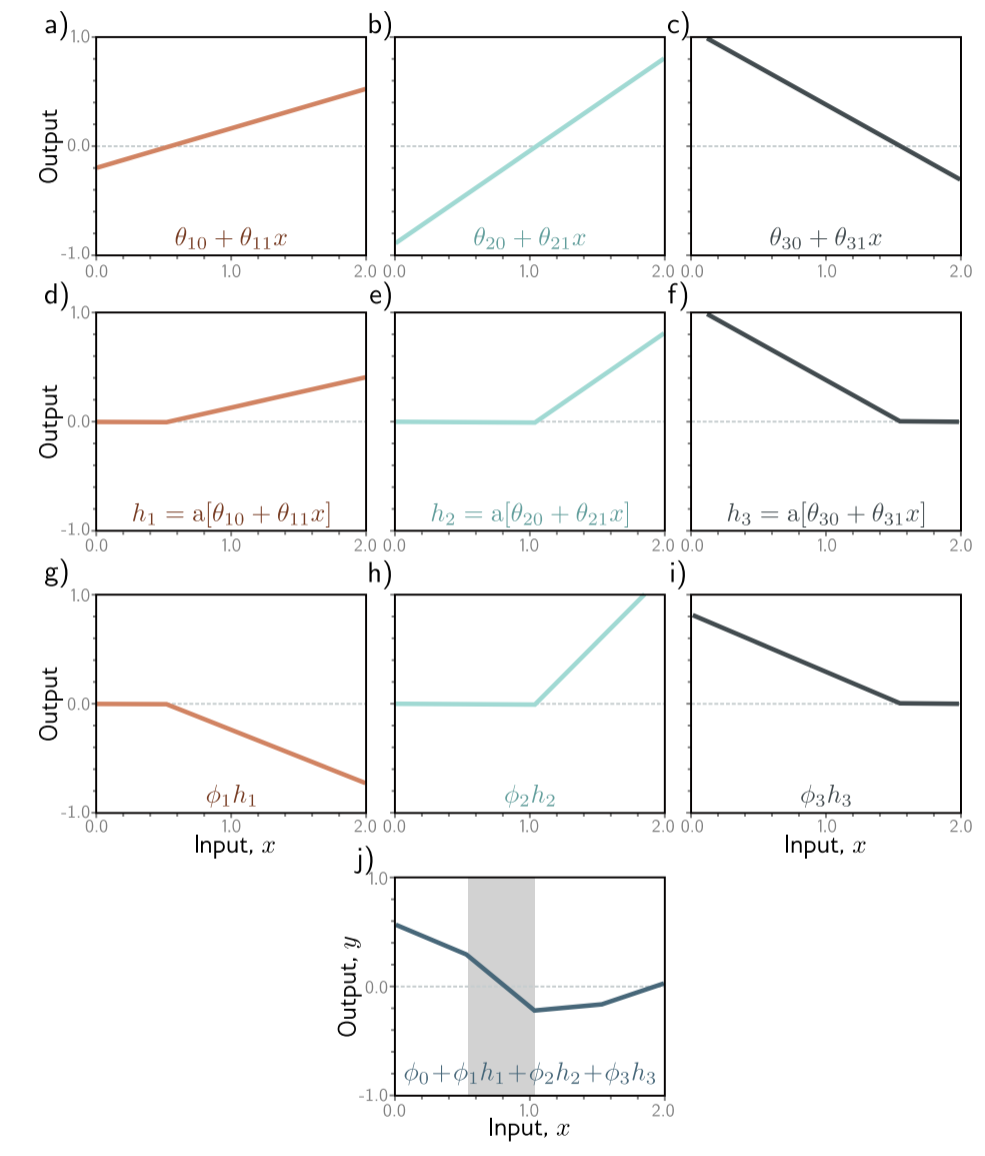
• 灰色区域内，只有节点1和节点3发挥作用，我们称这两个节点是活跃的，因为节点2为0，不做任何贡献（称为不活跃）。
• 三个隐藏单元将函数分为了四个区域（每个区域斜率不同），但是这四个区域中只有三个是相互独立的。

我们最后得到的浅层神经网络结构如下图：  

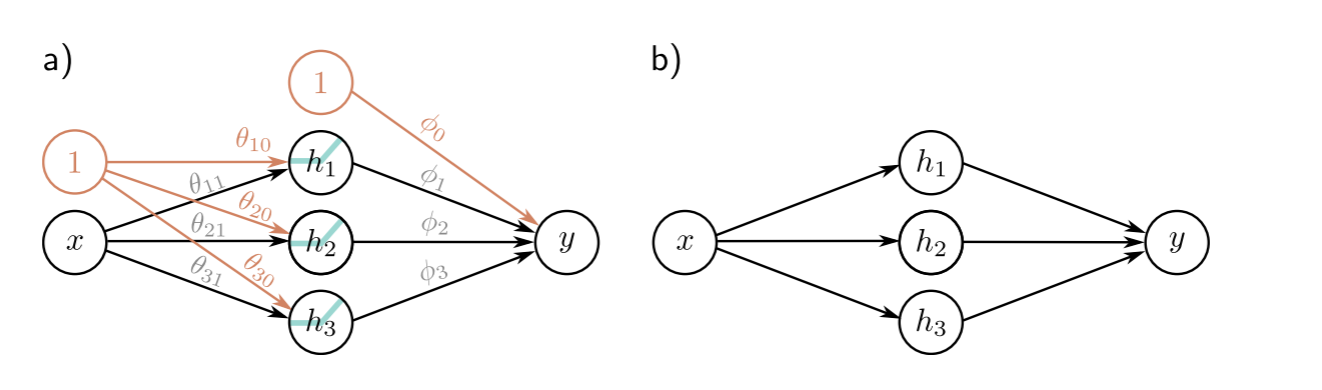
• 第一列称为输入层
• 第二列称为隐藏层
• 第三列称为输出层

Universal approximation theorem

通过上面我们可以知道，D个隐藏节点会生成D+1个区域。因此，我们可以通过添加隐藏节点的数量，分成任意大小、精度的区域，理论上能够完全模拟出任意一个函数。