2. Supervised Learning（监督学习）

2.1 Supervised Learning Overview（概述）

一、监督学习的基本目标
在监督学习（Supervised Learning）中，我们的目标是：构建一个模型$f$，它接收输入向量 $x$，输出预测结果向量 $y$。

为了简化起见，通常我们假设：

输入 $x$ 和输出 $y$ 都是固定大小的向量。
向量中的元素顺序固定,例如：
对于汽车示例，x 可能是[车龄, 行驶里程]，按顺序排列。

这类数据被称为 结构化数据（structured/tabular data）。
模型形式：$y = f(x)$,这表示我们希望通过函数 $f$ 来预测输出。

二、模型、参数与推理（Inference）
在实际中，模型不仅仅是 f(x)，它还有参数：
y = f(x, ϕ)
其中 $ϕ$ 是模型的参数，用于控制输入输出之间的映射关系。

推理（Inference）：使用训练好的模型进行预测的过程。

三、模型训练与损失函数
学习的目标:
找到使模型预测输出合理的参数 $ϕ$。

我们利用一个训练集，包含 I 个样本对：
${(x₁, y₁), (x₂, y₂), …, (xᵢ, yᵢ)}$

目标：
让每个输入 $xᵢ$ 都尽可能映射到正确的 $yᵢ$。

损失函数 Loss L
为了评估模型的好坏，我们定义了一个损失函数 $L(ϕ)$，用来衡量模型预测的输出与真实标签的差异。
损失函数越小，说明模型性能越好。

训练的本质是：寻找使损失最小的参数：

2.2 Linear regression example

让我们通过一个简单的例子来具体说明上述概念。
我们考虑一个模型：

y = f(x, ϕ)

它从一个输入 x 预测一个输出 y。我们将依次介绍：

模型的构建；
损失函数的设计；
模型的训练过程。

2.2.1 一维线性回归模型（1D Linear Regression Model）

一个 1D 线性回归模型 用一条直线描述输入 x 与输出 y 之间的关系。

其数学表达为：

y = f(x, ϕ)= ϕ₀ + ϕ₁·x
该模型包含两个参数： ϕ = [ϕ₀, ϕ₁]

ϕ₀：直线在 y 轴上的截距（y-intercept）
ϕ₁：直线的斜率（slope）

不同的参数组合会导致不同的输入-输出关系（如图 2.1 所示）：

斜率变化 → 直线倾斜程度变化
截距变化 → 直线上下平移

因此，公式 y = ϕ₀ + ϕ₁·x 实际上定义了一组可能的输入-输出关系（即所有可能的直线），而具体参数值则确定了这组关系中的某一条直线。

2.2.2 损失函数（Loss）

模型拟合优劣的衡量

图 2.2b~d 显示了由不同参数 ϕ 定义的三条拟合线。
图 2.2d 中的绿色线最接近数据点，因此拟合效果最好。
我们需要一种系统的方法来比较不同参数 ϕ 的好坏。

为此，我们使用一个数值来量化模型与真实数据之间的不匹配程度，这个值就叫： 损失（Loss）

损失越小，模型拟合效果越好。

不匹配的衡量方式

不匹配的量度来自以下差异：模型预测值 $f(xᵢ, ϕ)$ 与 真实标签 $yᵢ$ 的差

这些偏差在图中用橙色虚线表示。我们将所有训练样本的偏差平方求和，定义总损失为：

$L(ϕ) = ∑ (f(xᵢ, ϕ) − yᵢ)²= ∑_{i=1}^I (ϕ₀ + ϕ₁·xᵢ − yᵢ)²$

这个表达式被称为： 最小二乘损失（Least-Squares Loss）

平方操作的作用是消除误差的正负，使得所有误差都对最终结果产生贡献。
我们的目标是找到使损失最小的参数组合 $ϕ̂$，即：

$ϕ̂ = argmin₍ϕ₎ L(ϕ)
= argmin₍ϕ₎ ∑(f(xᵢ, ϕ) − yᵢ)²
= argmin₍ϕ₎ ∑(ϕ₀ + ϕ₁·xᵢ − yᵢ)²

由于该模型只有两个参数：

截距 ϕ₀ 和斜率 ϕ₁

我们可以计算在不同参数组合下的损失值，并将损失函数可视化为一个二维曲面图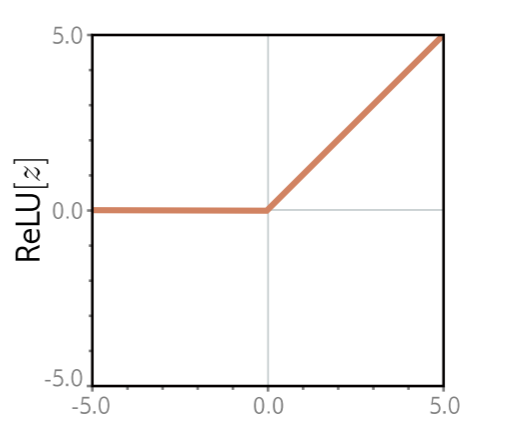

2.2.3 Training

最小化损失函数的过程称为 Model fitting（拟合）或 training（训练）或 learning（学习）

方法：梯度下降，测量当前位置的梯度，并朝着最陡峭的下坡前进，直到梯度平坦，无法下坡。

从数据中划分一部分数据作为测试数据，这一部分数据一般不参与到训练的过程中，输入数据经过模型得到输出的数据，再将数据数据与实际的数据作对比，得到最终的正确率。

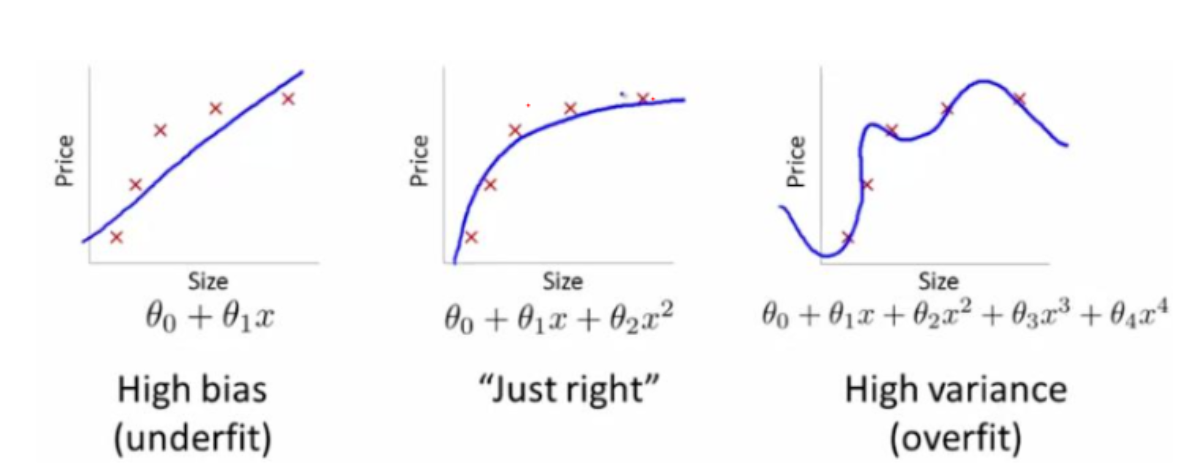
Underfitting（欠拟合）：模型不能够准确描述输入与输出直接的真是关系。
Overfitting（欠拟合）：数据中的存在一些非典型数据，最终导致了模型的异常检测。
{.is-success}

Chapter2