ml：逻辑回归

介绍

这是一个B站的逻辑回归讲解视频，但是没有详细讲解交叉熵损失是如何得到的。

逻辑回归主要用于二分类任务，分类任务与回归任务的区别主要是：回归任务的输出label是一个连续的值，二分类任务的输出label是离散的1或者0。

逻辑回归一开始我们还是使用和回归任务类似的线性模型输出一个值z，再将z输入到sigmoid函数中获得一个0-1之间的label（也就是y）,这个然后再通过一个跃迁函数来将这个label变化为0或1，这样就完成了一个分类任务。

$$
逻辑回归 = Sigmoid(线性模型输出)
$$

跃迁函数如下：

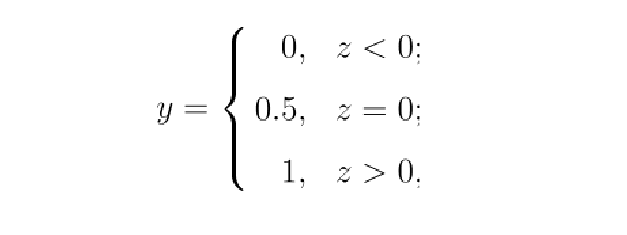
但是由于该函数是不连续的，我们无法用梯度下降来拟合该函数模型。因此我们选择Logistic(sigmoid) 函数用来近似跃迁函数，该函数是是连续可导.

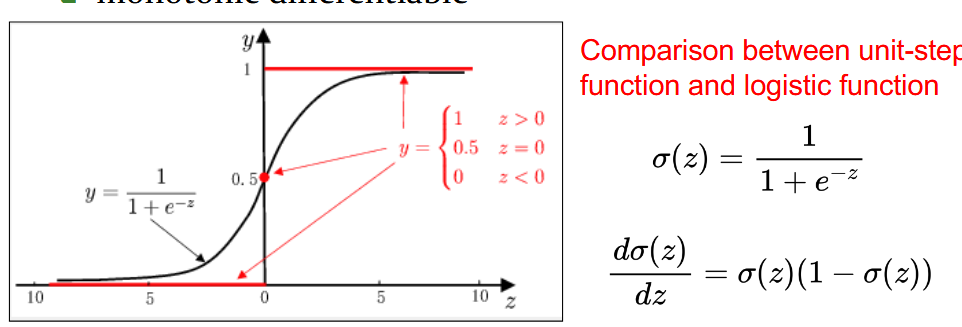
sigmoid函数的作用

为什么不能直接用线性输出的结果作为输入，再使用跃迁函数得到最后的分类结果

author: Gemini

这是一个非常深刻且关键的问题，直接触及了现代机器学习模型设计的核心思想。你的想法非常符合直觉，你所描述的模型（线性输出 + 跃迁函数）实际上就是最早的神经网络模型之一——感知机（Perceptron）。

它确实能进行分类，但在训练和性能上存在一些根本性的问题，而这正是Sigmoid（以及其他类似函数）被引入来解决的。

简单回答就是：因为跃迁函数（Step Function）是不可导的（或者说导数几乎处处为零），导致模型无法通过梯度下降法进行有效的学习。

下面我们来详细拆解这个问题。

你描述的模型：感知机 (Perceptron)

计算线性得分：z = wᵀx + b
应用跃迁函数：
- 如果 z ≥ 0，预测 ŷ = 1
- 如果 z < 0，预测 ŷ = 0

这个模型看起来简单、直接。但问题出在如何训练它。

核心问题：模型如何“学习”？

我们之前讨论过，模型学习的过程就像有一个“教练”（目标函数/损失函数）在指导。

模型做出一次预测。
“教练”评估这次预测有多糟糕（计算损失）。
“教练”需要告诉模型如何调整参数 w 和 b 才能在下一次做得更好。

这个“如何调整”的指令，就是梯度（Gradient）。梯度下降法的核心就是：参数 = 旧参数 - 学习率 * 损失函数对参数的梯度。

梯度告诉我们，参数往哪个方向调整，损失会下降得最快。

为什么跃迁函数无法提供有效的“指令”（梯度）？

让我们看看跃迁函数的形状和它的导数：

函数图像：它是一条在 z=0 处发生突变的“阶梯”。
导数（梯度）：
- 在 z > 0 的区域，函数是平的，导数为 0。
- 在 z < 0 的区域，函数也是平的，导数为 0。
- 在 z = 0 这个点，函数是垂直的，不可导（可以看作梯度无穷大）。

这对学习意味着什么？

梯度为0：假设你的模型预测错了。梯度下降法需要根据梯度来更新权重。但因为梯度是0，所以 学习率 * 0 = 0。参数的更新量也是0！模型根本不会更新参数，它学不到任何东西。 无论预测错得有多离谱，只要输出的 z 不是正好为0，模型都无法从错误中吸取教训。
不可导：在 z=0 这个点，梯度是无穷大，这会导致更新的数值爆炸，让整个训练过程变得极其不稳定。

用“教练”的比喻来说，使用跃迁函数的教练只会给出两种反馈：

“你没错，不用调整。”（梯度=0）
在极少数情况下，给出一个极其混乱、无法执行的指令。（梯度无穷大）

这样的教练无法指导一个模型进行细致、有效的学习。

Sigmoid 函数如何完美解决这些问题？

现在我们来看看Sigmoid函数的优点：

处处可导，梯度平滑：Sigmoid函数是一条平滑的曲线。在任何一点，你都可以计算出它的导数。这意味着，无论你的预测 ŷ 是0.1, 0.5, 还是0.9，总能计算出一个明确、有限的梯度。
提供有意义的梯度：
- 如果模型预测 ŷ = 0.6，但真实标签是 y = 1，Sigmoid函数和交叉熵损失会计算出一个梯度，告诉模型：“你需要调整参数，让 z 再大一点。”
- 如果模型预测 ŷ = 0.95，真实标签是 y = 1，它也会给出一个梯度，但这个梯度会比前一种情况小，因为它告诉模型：“你做得已经很好了，稍微调整一下就行。”
- 这种与误差程度成正比的反馈，使得学习过程非常高效和稳定。
输出是概率，衡量不确定性：Sigmoid的输出是一个0到1之间的概率值，这不仅用于分类，还告诉我们模型对这个预测的“信心”有多大。预测0.51和预测0.99都属于类别“1”，但前者表示模型非常不确定，后者表示非常确定。这个概率信息对于计算一个有意义的损失值（如交叉熵）至关重要。

总结

特性	跃迁函数 (Perceptron)	Sigmoid 函数 (Logistic Regression)
输出类型	确定的0或1（硬分类）	0到1之间的概率（软分类）
可导性	几乎处处导数为0，在0点不可导	处处可导，梯度平滑
学习能力	无法使用梯度下降法有效学习	非常适合梯度下降法
反馈机制	全有或全无，无法衡量“错的程度”	可以提供与误差大小成正比的、细致的反馈

结论：
我们之所以不直接用跃迁函数，不是因为它不能分类，而是因为它几乎无法被现代主流的、基于梯度下降的优化算法所训练。Sigmoid函数的引入，其最根本的意义就在于它是一个可导的、平滑的“代理”，它模仿了跃迁函数的行为（把数值压缩到0和1附近），但又完美地解决了梯度为零的问题，从而解锁了使用梯度下降法来高效训练分类模型的能力。

对于损失函数，如果我们使用MSE，我们发现我们得到的图像并不是凸函数，我们只能找到局部最优点，因此我们必须寻找其他的损失函数来操作。我们可以从概率的角度来推导交叉熵损失(cross-entropy loss)，更加详解的解释

常见的梯度下降很容易理解，下面介绍一下牛顿法求解

牛顿下降法

牛顿法的核心是利用一个二次函数来近似当前位置附近的损失函数，然后直接跳到这个二次函数的最低点。

单变量情况（更容易理解）

假设我们的目标函数是 f(x)，我们想找到它的最小值，也就是 f’(x) = 0 的点。
我们在当前点 xₜ 对函数 f(x) 进行二阶泰勒展开：

$f(x) ≈ f(xₜ) + f’(xₜ)(x - xₜ) + (1/2)f’’(xₜ)(x - xₜ)²$

这是一个关于 x 的二次函数。为了找到它的最小值，我们对它求导并令其为0：
$f’(xₜ) + f’’(xₜ)(x - xₜ) = 0$

我们求解这个方程来得到下一步的位置 x_{t+1}：
$x_{t+1} - xₜ = - f’(xₜ) / f’’(xₜ)$
$x_{t+1} = xₜ - f’(xₜ) / f’’(xₜ)$

这就是单变量牛顿法的更新公式。

f'(xₜ) 是梯度。

f''(xₜ) 是曲率。

多变量情况（机器学习中的应用）

在机器学习中，我们的参数是一个向量 θ，目标函数是 J(θ)。

一阶导数变成梯度向量 (Gradient)：∇J(θ)

二阶导数变成海森矩阵 (Hessian Matrix)：H，它是一个包含了所有二阶偏导数的方阵。

多变量的更新公式变为：
$θ_{t+1} = θₜ - H⁻¹ ∇J(θₜ)$

∇J(θₜ) 是梯度向量。

H⁻¹ 是海森矩阵的逆矩阵。除法在矩阵运算中对应于乘以逆矩阵。

多项式逻辑回归

核心思想： Softmax函数可以将一个包含任意实数（可正可负）的向量，转换成一个由0到1之间的数值组成的、并且所有值相加之和为1的概率分布向量。

输入 (Input)

一个 K 维的向量 z = [z₁, z₂, …, zₖ]。

在机器学习的分类任务中，这个向量 z 通常是模型（如神经网络或线性模型）对每个类别的原始预测分数，也称为 logits。K 代表类别的总数。

这些分数本身没有明确的意义，比如z₁=1.5，z₂=-0.8。我们无法直接将它们当作概率。
Softmax 公式详解

公式分为两步：

取指数 (Exponentiation)：对向量 z 中的每一个元素 zᵢ，计算 exp(zᵢ)，也就是 e^(zᵢ)。

    目的1：转为正数。因为概率不能是负数，exp 函数可以将任何实数（无论正负）都映射到一个正数。

    目的2：放大差异。指数函数是一个增长很快的函数。如果一个分数 zᵢ 比另一个分数 zⱼ 大一点，那么 exp(zᵢ) 会比 exp(zⱼ) 大很多。这有助于模型更“自信”地选择那个分数最高的类别。

归一化 (Normalization)：将上一步得到的每个 exp(zᵢ) 除以所有 exp(zⱼ) 的总和 Σ exp(zⱼ)。

    目的：使总和为1。这是概率分布最核心的性质。通过除以总和，我们确保了输出向量的所有元素加起来正好等于1。

输出 (Output)

输出是一个新的 K 维向量 softmax(z)。

这个输出向量的第 i 个元素 softmax(zᵢ) 可以被解释为：输入属于第 i 个类别的概率。

Softmax 是一个“分数转换器”，它将模型内部的原始、无限制的分数（logits）转换成一个符合我们直观理解的、关于所有类别的概率分布。

Softmax的直观示例

示例

输入向量 z (6个类别的原始分数): [0.6, 1.1, -1.5, 1.2, 3.2, -1.1]

观察输入：

 分数有正有负。

 最高的分数是 3.2（第5个类别）。

 最低的分数是 -1.5（第3个类别）。

输出向量 softmax(z) (转换后的概率): [0.055, 0.090, 0.006, 0.099, 0.74, 0.010]

观察输出：

 所有值都在0和1之间。

 所有值的总和为1（0.055 + 0.090 + ... + 0.010 = 1.0）。

 原始分数最高的类别（3.2），现在拥有了压倒性的最高概率（0.74，即74%）。

 原始分数最低的类别（-1.5），现在的概率几乎可以忽略不计（0.006，即0.6%）。

 即使是原始分数第二高的 1.2，其最终概率 0.099 也远低于最高的 0.74。

“锐化” (Sharpen) 效应

右侧的图示非常形象地解释了这个过程。Softmax就像一个**“锐化”**工具。

它接收一组比较分散的原始分数（图中的”Average”），然后输出一个“贫富差距”极大的概率分布（图中的”Sharpen”）。

这个特性被称为**“赢家通吃”（Winner-takes-all）**。Softmax会不成比例地放大最高分数的优势，同时抑制其他所有分数。
与Sigmoid的类比

Softmax就像Sigmoid函数一样，有“挤压”数值的作用。

Sigmoid：将一个任意实数挤压到0和1之间，用于二元分类（是/否）。

Softmax：将一个向量的任意实数挤压成一个总和为1的概率分布，用于多项式（多类别）分类（猫/狗/鸟…）。

因此，Softmax可以被看作是Sigmoid函数在多类别情况下的推广和延伸。