Harris Detector
1.Background
Motivation:panorama stitching(全景拼接)
- 特征提取
- 匹配特征
- 对其图像
characteristics of good features
- repeatability 重复性
- saliency 相对性
- Compactness and efficiency 紧凑性和效率
- locality 局部性
Corner:
- 性质:在角落的周围,图像的梯度有两个或者多个主导的方向
- 角落是可以重复和识别的
2.Corner Detection
“如果一个点是角点,那么我们在它周围移动一个小窗口,无论向哪个方向移动,窗口内的图像像素值都会发生很大的变化。”
$ E(u, v) = \sum_{x,y} w(x, y) [ I(x+u, y+v) - I(x, y) ]^2 $
一旦发生位移,差异($ E $值)迅速变大。这说明该点极有可能是个角点。
- Window function(窗口函数):
- 矩形窗(Box/Flat):图左下的方形图。窗口内的权重为1,窗口外为0。也就是简单粗暴地把窗口内的像素差异加起来。缺点是移动窗口时,边缘进出的像素会导致 $ E $ 值突变,不够平滑。
- 高斯窗(Gaussian):图右下的钟形曲线。中心权重高,边缘权重低。这是一种更常用的方式,因为通过给中心像素更高的权重,可以降低噪声的影响,并且让计算出的 $ E $ 值变化更平滑(各向同性)。
3.二次近似
3.1 数学表达一
$ E(u, v) \approx \begin{bmatrix} u & v \end{bmatrix} M \begin{bmatrix} u \ v \end{bmatrix} $
- 含义:它告诉我们,对于微小的位移 $ (u, v) $,图像灰度的变化量 $ E $ 可以近似看作是一个关于 $ u $ 和 $ v $ 的二次函数。
- 几何意义:如果你把 $ E(u,v) $ 画成三维地形图,这就相当于在原点附近用一个**椭圆碗(抛物面)**来拟合原本复杂的地形。
- 关键点:所有的形状特征信息,现在都浓缩在了中间那个 $ 2 \times 2 $** 的矩阵 **$ M $ 里面。
矩阵 $ M $ 的核心内容:
$ M = \sum_{x,y} w(x, y) \begin{bmatrix} I_x^2 & I_x I_y \ I_x I_y & I_y^2 \end{bmatrix} $
这个矩阵在计算机视觉中非常有名,通常被称为*结构张量(Structure Tensor)或自相关矩阵*。让我们拆解它的成分:
- $ I_x $** 和 $ I_y $:这是图像在 $ x $ 方向和 $ y $ 方向的导数(梯度)**。
- $ I_x $:水平方向的像素变化率。
- $ I_y $:垂直方向的像素变化率。
- 右侧的小方框图示:
[-1 1]:这是计算 $ I_x $ 的简单卷积核(右边像素减左边像素)。[-1; 1](竖着的):这是计算 $ I_y $ 的卷积核(下边像素减上边像素)。
- 矩阵元素:
- $ I_x^2 $:水平梯度的平方。如果图像有垂直边缘(左右像素差异大),这个值会很大。
- $ I_y^2 $:垂直梯度的平方。如果图像有水平边缘(上下像素差异大),这个值会很大。
- $ I_x I_y $:水平和垂直梯度的乘积。这反映了两个方向梯度的相关性。
- $ \sum w(x, y) $:和上一张PPT一样,这代表我们在窗口内对这些梯度值进行加权求和(平滑噪声)。
3.2 数学表达二
$ M $ 的另一种数学表达,强调了它是由梯度向量 $ \nabla I $ 的外积构成的。
$ M = \sum (\nabla I)(\nabla I)^T $
这一步的意义在于将“寻找角点”转化为了“分析矩阵 $ M $ 的特征值”:
- 平坦区域:图像几乎没变化,导数 $ I_x, I_y $ 都接近0。$ \rightarrow $ 矩阵 $ M $ 的值都很小。
- 边缘区域:
- 如果是竖直线,只有 $ I_x $ 大,$ I_y $ 小。
- 如果是水平线,只有 $ I_y $ 大,$ I_x $ 小。
- $ \rightarrow $ 矩阵 $ M $ 只有一个显著的大特征值。
- 角点区域:
- 角点意味着在两个方向上都有剧烈变化。
- $ I_x $ 和 $ I_y $ 都很大。
- $ \rightarrow $ 矩阵 $ M $ 的两个特征值都很大。
几何表达
1.从公式到几何图形(椭圆)
- 水平切片(Horizontal Slice):
回忆一下,之前说 $ E(u, v) $ 像是一个碗(抛物面)。如果我们用一把刀水平切开这个碗(让 $ E(u, v) = \text{const} $ 常数),切口的形状就是一个椭圆。
公式 $ [u \ v] M [u \ v]^T = \text{const} $ 正是椭圆的方程。 - 对角化(Diagonalization):
公式 $ M = R^{-1} \begin{bmatrix} \lambda_1 & 0 \ 0 & \lambda_2 \end{bmatrix} R $ 展示了线性代数中的特征值分解。- $ R $:旋转矩阵。它决定了椭圆是斜躺着还是正放着(也就是梯度的方向)。
- $ \lambda_1, \lambda_2 $(特征值):它们决定了椭圆的长轴和短轴的长度(也就是梯度的大小)。
- 右下角椭圆图解(核心难点)
这是整张图最需要理解的部分,因为它展示了特征值($ \lambda $)与图像变化快慢的反比关系:
- $ \lambda $** 代表什么?**
$ \lambda $(特征值)代表图像在某方向上的变化剧烈程度。$ \lambda $ 越大,变化越剧烈(山坡越陡)。 - 为什么椭圆轴长是 $ \lambda^{-1/2} $?
- 如果某个方向变化非常剧烈($ \lambda $ 很大,山很陡),那么你稍微移动一点点距离,高度差($ E $)就很大了。为了保持高度差恒定(const),你在该方向只能移动很短的距离。
- 结论:
- 蓝箭头(短轴):对应 $ \lambda_{max} $(大特征值)。这是图像变化最快的方向(Fastest change)。
- 红箭头(长轴):对应 $ \lambda_{min} $(小特征值)。这是图像变化最慢的方向(Slowest change)。
- 如何用这个椭圆判断“角点”?
通过观察这个椭圆的形状(也就是比较 $ \lambda_1 $ 和 $ \lambda_2 $ 的大小),我们可以判断当前像素点属于哪种图像特征:
- 角点(Corner):
- 特征:无论往哪个方向动,变化都很快。
- 数学:两个特征值 $ \lambda_1 $ 和 $ \lambda_2 $ 都很大。
- 形状:椭圆很小,且接近圆形(蓝箭头和红箭头都很短)。
- 边缘(Edge):
- 特征:沿边缘移动变化慢,垂直边缘移动变化快。
- 数学:一个特征值很大($ \lambda_1 $),另一个很小($ \lambda_2 \approx 0 $)。
- 形状:椭圆极其细长(一个轴很短,另一个轴很长)。
- 平坦区域(Flat Region):
- 特征:往哪动都没啥变化。
- 数学:两个特征值 $ \lambda_1 $ 和 $ \lambda_2 $ 都很小。
- 形状:椭圆非常巨大(甚至可能是发散的)。
寻找角点 $ \approx $ 寻找矩阵 $ M $ 的两个特征值都很大的区域。
只有那些在两个方向上梯度变化都很剧烈的地方(比如窗户角、建筑轮廓转折点),才会被标记为角点
4.角点响应函数
我们已经知道要通过矩阵 $ M $ 的特征值 $ \lambda_1 $ 和 $ \lambda_2 $ 来判断是不是角点。但是,直接计算特征值(涉及开平方根)在计算上是非常耗时的。
Harris 提出了一种巧妙的方法,通过定义一个评分函数 $ R $,不需要计算特征值本身,就能直接判断角点。
以下是详细解读:
- 公式解读
$ R = \det(M) - \alpha \cdot \text{trace}(M)^2 $
这个公式利用了线性代数的两个性质:
- $ \det(M) = \lambda_1 \lambda_2 $:矩阵的行列式等于特征值的乘积。
- $ \text{trace}(M) = \lambda_1 + \lambda_2 $:矩阵的迹(对角线元素之和)等于特征值之和。
- $ \alpha $** (常数)**:通常取值为 0.04 到 0.06。它是一个经验参数,用来调节检测的灵敏度。
A. “Corner” 角点区域(绿色)
- 数学特征:$ \lambda_1 $ 和 $ \lambda_2 $ 都很大。
- $ R $** 值表现**:
- $ \lambda_1 \lambda_2 $ (乘积)非常大。
- 虽然 $ (\lambda_1 + \lambda_2)^2 $ 也大,但因为乘了一个很小的系数 $ \alpha $(0.04),所以第一项 $ \det(M) $ 占主导地位。
- 结果:$ R $** 是很大的正数 ($ R > 0 $)**。
B. “Edge” 边缘区域(橙色)
- 数学特征:一个特征值很大,另一个很小(比如 $ \lambda_1 \gg \lambda_2 \approx 0 $)。
- $ R $** 值表现**:
- $ \det(M) = \lambda_1 \lambda_2 \approx 0 $(因为有一个接近0)。
- $ \text{trace}(M)^2 = (\lambda_1 + 0)^2 = \lambda_1^2 $(是个大数)。
- 公式变成:$ Small - \alpha \cdot Large $。
- 结果:$ R $** 是负数 ($ R < 0 $)**。
C. “Flat” 平坦区域(灰色)
- 数学特征:$ \lambda_1 $ 和 $ \lambda_2 $ 都很小。
- $ R $** 值表现**:
- 乘积很小,和也很小。
- 结果:$ R $** 的绝对值很小 ($ |R| \approx 0 $)**。
这就是 Harris 角点检测的最后一步“判决”过程:
- 对图像中的每个像素,算出它的 $ R $ 值。
- 如果 $ R > \text{Threshold} $(某个设定的阈值),且 $ R $ 是局部最大值,那么这个像素就是角点。
- 如果 $ R < 0 $,它是边缘。
- 如果 $ R \approx 0 $,它是平坦区域。
这种方法既避开了复杂的特征值计算,又完美区分了角点、边缘和平坦区域。

5.不变性和协变性
- 核心目标
- 对光照变换(Photometric transformations)保持不变性(Invariant)。
- 对几何变换(Geometric transformations)保持协变性(Covariant)。
- 不变性(Invariance)—— 针对光照
- 定义:当图像发生某种变换(通常指像素值的变化,如亮度、对比度)时,角点的位置和检测结果不发生改变。
- 场景(Photometric):比如天黑了、开灯了、或者曝光度改变了。
- 图解分析:
- 看左边的牛(亮)和右边的牛(暗)。
- 虽然右边的图像整体变暗了(像素值变了),但算法依然要在牛身上同样的位置找到红色的角点。
- 如果图像变暗导致角点消失了,那这个算法就很差劲。Harris 角点检测通常对亮度平移(整体变亮变暗)是具有不变性的。
- 协变性(Covariance)—— 针对几何形状
- 定义:如果如果对图像进行了几何变换(如旋转、平移),检测到的特征点应该随之发生相应的移动。
- 场景(Geometric):比如物体移动了、旋转了。
- 图解分析:
- 看左边的牛是直立的,右边的牛是倾斜的(旋转了)。
- 我们不希望特征点“保持不变”(如果不通过变,特征点就会悬浮在原来的坐标 $ (x,y) $ 上,脱离了牛的身体)。
- 我们希望特征点能跟着牛一起转。
- “Covariance”的意思就是“共变”:牛转了,角点坐标也跟着转。这样我们才能说,右图牛耳朵上的点,对应左图牛耳朵上的点(Corresponding locations)。
Harris 角点检测的表现:
- 光照(强度平移):部分不变(很好)。
- 旋转:协变(很好,旋转后特征值 $ \lambda $ 不变,椭圆跟着转,所以角点依然会被检测到)。
- 缩放(Scale):不具备协变性(这是Harris算法的一个大弱点,如果把图像放大,角点可能会变成边缘)。
如果照片的亮度或对比度变了,Harris 角点检测算法还能正常工作吗?
这在数学上被称为仿射强度变换(Affine Intensity Change),公式为:
$ I \rightarrow a I + b $
其中:
- $ I $:原始像素值。
- $ b $:亮度(Brightness)。相当于给所有像素加一个常数(比如整体变亮或变暗)。
- $ a $:对比度(Contrast)。相当于缩放像素值的差异(比如让黑的更黑,白的更白)。
这张图得出的结论是:Harris 算法对亮度变化完全免疫,但对对比度变化比较敏感(即“部分不变”)。
- 对亮度平移 ($ + b $) 完全不变
- 原理:
Harris 算法的核心是计算图像的导数(梯度),比如 $ I_x = \frac{\partial I}{\partial x} $。
根据微积分基本原理,常数的导数为 0。
$ \frac{\partial (I + b)}{\partial x} = \frac{\partial I}{\partial x} + 0 $
- 结论:
无论你把图片整体调亮还是调暗(只要不过曝或全黑),图像的梯度值完全不变,算出来的角点响应值 $ R $ 也不变。所以算法能完美找到同样的角点。
- 对对比度缩放 ($ \times a $) 不完全不变
- 原理:
如果你改变对比度(乘以系数 $ a $),导数也会随之改变:
$ \frac{\partial (aI)}{\partial x} = a \frac{\partial I}{\partial x} $
- 这意味着计算出来的角点响应值 $ R $ 也会随之变大或变小。
- 图解分析(左右两个波形图):
- 图中的曲线代表计算出的角点响应值 $ R $。
- 灰色区域(Threshold):这是我们要设定的阈值线。只有波峰超过这条线,才会被认定为“角点”。
- 左图(原始图像):有 3 个红点超过了阈值,被检测为角点。
- 右图(对比度增强后):
- 图像对比度增加($ a > 1 $),所有的波峰都变高了。
- 原来的 3 个红点依然被检测到了(没问题)。
- 问题来了:原本有一个没达到阈值的波峰(左图中被淹没的),现在因为整体“水位”上涨,冲过了阈值线(变成了右图中的绿点)。
- 这意味着:对比度增强可能会导致算法检测出一些“伪角点”;反之,对比度降低可能会导致原本的角点“消失”。
Covariant
- Image translation(图像平移)
Harris仍然能够起作用,因为窗口是不断平移检测的,而我们的角点又只和邻域的像素有关
- Image rotation(图像旋转)
不会改变,因为旋转在由参数 $ R $控制,而我们角点是通过$ M $来确定
❌**** Covariant
Scaling(缩放)
会改变,放大后一些角点会变成边缘
Blob detection
斑点检测
Scale is important
假设我们在寻找一个角点,如何确定窗口的大小是一件很难的事情
Scale Invariant Detection
如果我们要对两个尺度不一样的图片进行匹配,存在两个问题:
- 如何在两个图片里面独立的寻找出两个匹配的区域(假设区域是圆,我们如何确定两个图片里面圆的大小)
- 如何寻找两个图片之间的联系
Solution:我们需要寻找一个机制来寻找尺度缩放图片中的相同的特性或特征,设计一个在相同区域上工作的“尺度不变性”的函数
Key Point : Consistent context(e.g average intensity)
核心思想:不再使用固定大小的窗口,而是去寻找每个特征点的“最佳尺寸”
常用方法:取局部最大值(这个局部最大值的区域是随着图像缩放covariant)
一个好的scale invariant function应该只有一个稳定的局部最大值
Find Function
Laplacian:高斯函数的二阶导数
边缘:一条波纹
斑点:两条波纹的叠加
空间选择:只要拉普拉斯算子的尺度与斑点(blob)的尺度相“匹配”,拉普拉斯响应的幅度就会在斑点中心达到最大值
Scale selection
寻找斑点的特征尺度(scale characteristic)
- 利用不同尺度的Laplacians做卷积(当 $ \sigma $越大,丢失的边缘信息越多)
- 寻找响应最大的
结论:当 $ \sigma $增大到某个值的时候,滤波器的响应最大,这个$ \sigma $我们就称为斑点的特征尺度
Scale Normalization(尺度归一化)
问题:由于高斯滤波的总权重是一定的,当我们的 $ \sigma $变大的时候,高斯函数对应的值$ \frac{1}{\sigma \sqrt{2 \pi}} $也会变小,导致最后的响应值变小。——简而言之,高斯滤波器导数对理想阶梯边缘的响应随着$ \sigma $的增大而减小
Solution:为了保持响应程度相同,我们需要乘高斯导数$ \sigma $; 如果使用拉普拉斯,我们就要乘$ \sigma ^2 $
LoG
高斯-拉普拉斯算子(Laplacian of Gaussian, LoG),也被戏称为“墨西哥草帽”算子。
普通 LoG
公式为:
$ \nabla^2 g = \frac{\partial^2 g}{\partial x^2} + \frac{\partial^2 g}{\partial y^2} $
- 这是标准的定义:先用高斯函数 $ g $ 模糊图像,然后分别对 $ x $ 和 $ y $ 求二阶导数并相加(这就是拉普拉斯算子 $ \nabla^2 $ 的定义)。
尺度归一化 LoG
公式变为:
$ \nabla^2_{norm} g = \sigma^2 \left( \frac{\partial^2 g}{\partial x^2} + \frac{\partial^2 g}{\partial y^2} \right) = \sigma^2 \nabla^2 g $
- 关键变化:多乘了一个 $ \sigma^2 $。
- 为什么要乘 $ \sigma^2 $?(之前一维是乘 $ \sigma $,为什么二维是 $ \sigma^2 $?)
- 因为在二维高斯函数中,幅值随着 $ \sigma $ 的增加而衰减的速度是 $ 1/\sigma^2 $。
- 为了抵消这种衰减,让大斑点和小斑点在检测时能有“公平的待遇”,我们必须乘上 $ \sigma^2 $ 进行补偿。
Scale Selection
“At what scale does the Laplacian achieve a maximum response to a binary circle of radius r?”
(对于一个半径为 $ r $ 的黑白圆形斑点,拉普拉斯算子在什么尺度 $ \sigma $ 下能获得最大响应?)
为了让乘积之和(卷积响应)最大,滤波器的形状必须完全贴合圆形的边缘。也就是:拉普拉斯滤波器的“过零点”,必须正好落在圆形的边缘(半径 $ r $)上。
数学推导
拉普拉斯算子(LoG)的数学表达式:
$ (x^2 + y^2 - 2\sigma^2) e^{-(x^2+y^2)/2\sigma^2} $
我们要找**“过零点”**,也就是让这个式子等于 0。
指数部分 $ e^{(\dots)} $ 永远不为 0,所以只能是前面的括号部分为 0:
$ x^2 + y^2 - 2\sigma^2 = 0 $
- 我们知道圆的边缘位置是半径 $ r $,也就是 $ x^2 + y^2 = r^2 $。
- 代入进去:
$ r^2 - 2\sigma^2 = 0 $
$ r^2 = 2\sigma^2 $
$ r = \sigma\sqrt{2} $
我们得到最终的尺度选择公式:
$ \sigma = \frac{r}{\sqrt{2}} $
Scale-space blob detector
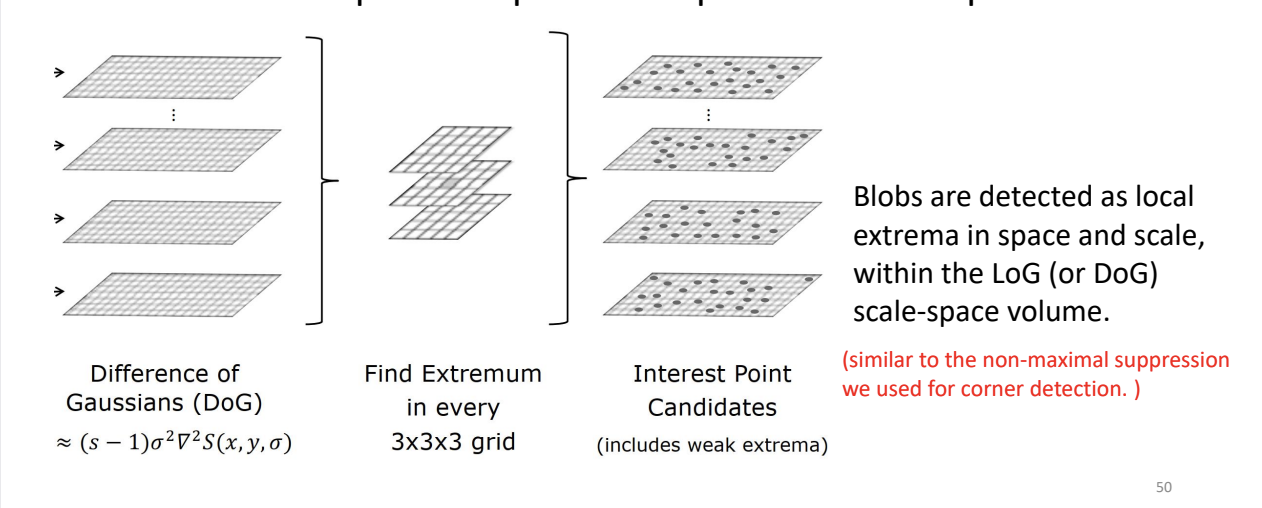
- 构建尺度空间(左图:Difference of Gaussians)
我们在之前的 PPT 里一直在讲 LoG (Laplacian of Gaussian) 是最好的斑点检测器。但是,在实际计算中,算 LoG 是很慢的(要对图像做卷积,还要算二阶导数)。
聪明的计算机视觉科学家(Lowe)发现了一个数学巧合:
“高斯差分 (Difference of Gaussians, DoG)” ≈ “归一化的 LoG”
- 什么是 DoG?
就是把一张图用 $ \sigma_1 $ 模糊一下,再用 $ \sigma_2 $ 模糊一下($ \sigma_2 > \sigma_1 $),然后把两张图相减。
$ DoG = Image_{\sigma_2} - Image_{\sigma_1} $
- 这只需要做减法,速度极快!
- 左边的叠层图:
这就代表了尺度空间金字塔。每一层都是不同模糊程度($ \sigma $)的 DoG 图像。我们不再在一张图上找,而是在这一堆图里找。
- 寻找极值(中间图:3x3x3 grid)
这是这张图最核心的操作:如何在三维空间 ($ x, y, \sigma $) 中找最大值?
我们要判断一个像素点是不是“斑点中心”,不仅要看它在当前图片里是不是最亮的,还要看它在尺度的维度上是不是最强的。
具体操作是检查 26 个邻居:
- 当前层 (Current Scale):查看它周围的 8 个邻居。
- 上一层 (Scale Above):查看它上面那层对应的 9 个邻居(更模糊的图)。
- 下一层 (Scale Below):查看它下面那层对应的 9 个邻居(更清晰的图)。
- 8 + 9 + 9 = 26。
判定规则:
只有当这个像素点的值,比这就 26 个邻居都大(或者都小)时,它才会被选为候选点。
这就是幻灯片里写的:“Find Extremum in every 3x3x3 grid”。
- 筛选候选点(右图:Interest Point Candidates)
- 经过上面的筛选,那些保留下来的点(右图中的黑点),就是我们要找的 Keypoints(关键点)。
- 每一个点包含三个信息:
- $ x $** 坐标**
- $ y $** 坐标**
- $ \sigma $** (尺度)**:它是在哪一层被检测出来的,就代表它的大小是多少。
Improve Efficiency
Problems:
- 全局空间搜索,每一个尺度都需要检测
- 当 $ \sigma $增加的时候,卷积计算的时间会增加
Solution 1: Harris Laplacian
- 寻找局部最大值:
- First Harris Corner Detection in space
- Then Laplacian Scale in specific space
Solution 2: SIFT
- 不直接使用LoG计算
- 用前面提到的DoG(高斯差分)计算减少计算量
How to detect different scale blobs?
我们可以使用不同尺度的卷积核,但是当我们使用大卷积的时候增加了计算复杂度,我们该如何改进?
From input view:
- 用多个小高斯卷积代替大卷积(e.g. 如果我们需要得到 $ k\sigma $的卷积结果,我们可以在$ \sigma $的结果上,再次使用 $ \sqrt{(k\sigma)^2 - \sigma ^2} $的高斯卷积)
- Down-sample(降采样)根据covariant的性质,将图片按比例缩小。我们可以继续进行降采样,构造不同的高斯列群和高斯差分群。
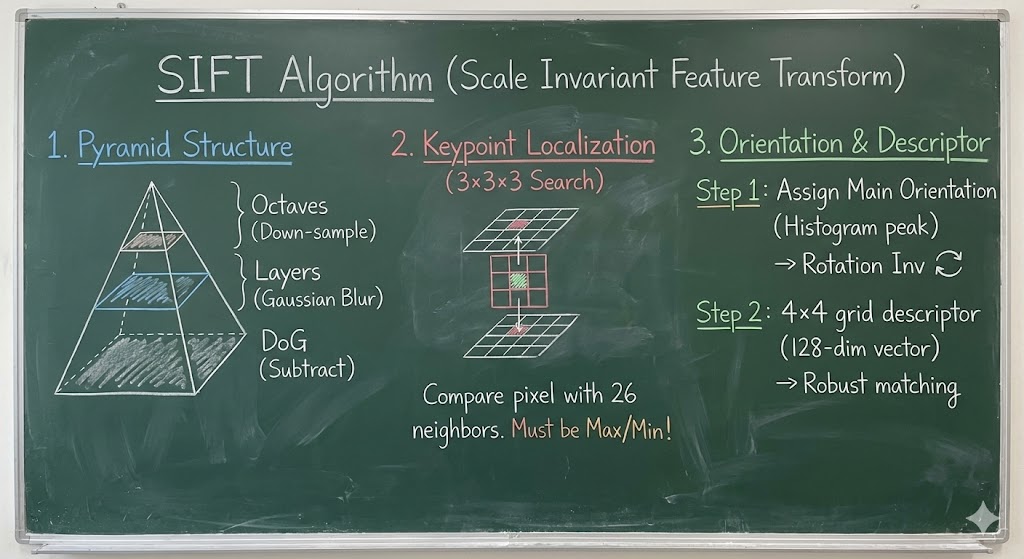
SIFT算法具体流程

这张幻灯片是 SIFT 算法实现的终极蓝图。它把之前讲的所有零碎知识点(高斯模糊、DoG、降采样、尺度空间)全部串联起来,展示了 SIFT 具体的金字塔架构。
要看懂这张图,你需要理解三个核心概念:Octave(组/阶)、Layer(层),以及参数 $ s $ 和 $ k $。
以下是详细拆解:
1. 宏观架构:高斯金字塔
看最右边的虚线塔状图:
- 整个处理过程被分成了若干个组 (Octaves)。
- Octave 1 (最底层):处理原尺寸图像。
- Octave 2 (往上一层):将图像**降采样(Down-sample)**一半,处理 1/2 大小的图像。
- Octave 3 (再往上一层):再降采样一半,处理 1/4 大小的图像。
- 目的:这就是之前说的“通过缩小图像来模拟大尺度滤波器”,为了加速。
2. 微观架构:DoG 层
看左边的 Gaussian 和中间的 Difference of Gaussians (DoG):
- 在每一个 Octave 内部,图像大小是不变的。
- 我们生成一系列模糊程度递增的高斯图像:$ \sigma, k\sigma, k^2\sigma, \dots $。
- 相邻两张高斯图相减,得到 DoG 图。
- 特征检测:我们在 DoG 图上寻找极值(斑点)。
3. 核心参数:$ s$ 和 $ k $
这是这张图最数学、也是最精妙的部分。
- $ s $ (Steps):
- 意思是我们希望在尺度翻倍(从 $ \sigma $ 到 $ 2\sigma $)的过程中,有多少个有效的检测层。
- 比如 $ s=2 $,意味着我们在尺度变大一倍的过程中,要检测 2 次。
- $ k $ (Factor):
为什么要这样设计?
是为了保证尺度的连续性。
当一个 Octave 结束时,尺度正好变成了 $ 2\sigma $。此时我们把图像缩小一半(降采样),图像里的特征也缩小了一半,所以下一组 Octave 的初始尺度又相当于回到了起点,可以无缝衔接。
- 这是每次模糊增加的倍数。
- 公式:$k = 2^{1/s}$。
- 原理:因为我们要经过 $s$ 次乘法($ k \times k \times \dots $)后,尺度正好翻倍(变成 $ 2 $)。即 $ k^s = 2 $,所以 $ k = 2^{1/s}$。
4. 为什么是 “S+3” 张高斯图?
看左下角的红字:”S+3 Gaussian” $ \rightarrow $ “S+2 DOG”。
这是为了解决边界问题:
- 我们要检测 $ s $ 个尺度的极值。
- 要在 3D 空间(上下层)找极值,每一层都需要“有上家、有下家”才能比较 。
- 所以,为了检测 $ s $ 层,我们需要 $ s+2 $ 层 DoG(头尾两层 DoG 只能做陪衬,用来提供比较值,自己不能被选为极值)。
- 而 DoG 是由高斯相减得到的($ N $ 张高斯只能产生 $ N-1 $ 张 DoG)。
- 结论:为了得到 $ s $ 个有效检测层,我们需要 $ s+2 $ 张 DoG,进而需要 $ s+3 $ 张高斯图。
Invariance and covariant properties
Laplacian(Blob)对旋转和缩放不变
Blob 的位置和尺度是covariant
但是对于光照强度不是不变的,对于亮度平移保持不变$ +b $,但是对于对比度缩放是线形变化的 $ \times a $
From convariant detection to invariant description
A:尺度归一化
我们在两张图中的特征圈大小不一样,我们可以缩放到相同大小的标准圈,就可以完成尺度的归一化
B:仿射归一化
Question:我们两个图中的椭圆的大小、旋转角度和形状都不一样
Solution:我们可以将椭圆拉成单位圆,我们可以顺时针也可以逆时针拉,但是圆的旋转角度是不一样。因此我们需要找到一个主方向,把圆旋转到一个固定的角度。
如何寻找主方向:我们计算每一个像素的梯度方向,并切用直方图统计,选择直方图最高的作为主方向
**特征描述子:*我们需要将图像划分为多个窗口,其中44的窗口是最合适的。如果划分越细,表示越准确,但是可能无法匹配;如果划分越粗,表示越模糊,但是可能产生多个匹配的结果
SIFT的核心目标:
- invariant:
无论图片怎么缩放和旋转,我们提取的特征向量是一模一样的
- covariant
如果图片旋转了,那么我们的特征框也必须要旋转
Person detector
Histogram Oriented Gradients
局部物体外观和形状往往能够很好的描述为局部强度梯度的分布或边界方向
具体步骤:
- 将图像分割成多个cell 区域
- 每个cell计算各个方向的梯度
- 拼接直方图
- 块归一化(overlab)
Advantage:
- 局部形状信息
- 对于局部几何变换和光照变换的invariant
Disadvan:
- 遮挡
- 旋转和缩放(我们没有选取主方向)
- 噪声(梯度对噪声敏感)
HoG vs. SIFT
- HoG 用于描述整个图像,SIFT用于关键点匹配
- SIFT直方图是朝向主方向(主梯度),HoG不是
- 使用邻域bins对HoG梯度归一化
- SIFT用不同的尺度来计算多个描述子